A Study on ANN/RNN-based Photovoltaic Generation Forecasting

Su Wung Baek; Sung Gi Kwon; Chang Heon Kim; Gye Choon Park

doi:10.21218/CPR.2024.12.3.049

Preview

Current Photovoltaic Research. 30 September 2024. 49-54
https://doi.org/10.21218/CPR.2024.12.3.049

A Study on ANN/RNN-based Photovoltaic Generation Forecasting

ANN/RNN 기반 태양광 발전량 예측에 관한 연구

Su Wung Baek¹

Sung Gi Kwon²

Chang Heon Kim³^*

Gye Choon Park⁴^**

백 수웅¹

권 성기²

김 창헌³^*

박 계춘⁴^**

¹Department of Electrical Engineering, Mokpo National University, Muan-gun, 58554, Korea / Enterprise Support Division, Energy Valley Enterprise Development Institute, Naju-si, 58324, Korea

²Department of Electrical Engineering, Mokpo National University, Muan-gun, 58554, Korea

³Artificial Intelligence & Energy Research Center, Korea Photonics Technology Institute, Gwangju, 61007, Korea

⁴Department of Electrical Engineering, Mokpo National University, Muan-gun, 58554, Korea

¹전기공학과, 목포대학교, 무안군, 58554 / 기업지원실, 에너지밸리기업개발원, 나주시, 58324

²전기공학과, 목포대학교, 무안군, 58554

³AI에너지연구센터, 한국광기술원, 광주광역시, 61007

⁴전기공학과, 목포대학교, 무안군, 58554

^{*Corresponding Author}

^{**Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/4.0/):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

This study proposed a forecasting model that combines ANNs and RNNs to address the intermittency and fluidity of solar power generation. Four prediction models were trained separately based on sky conditions provided by the Korea Meteorological Administration, and insolation was estimated using the ASHRAE Clear-Sky model. The proposed model showed an error rate of 6.5-7.7% based on NMAE, which meets the requirements of power generation prediction. As a result, this study can improve the accuracy of solar power generation forecasting, which can contribute to the stability of power operation and the profitability of power operators.

Keywords

Photovoltaic generation forecasting

ANN

RNN

Solar radiation

Forecast model

MAIN

Nomenclature
Subscript
1. 서 론
2. 연구 방법
2.1 대기 상태에 따른 예측 모델 분리
2.2 일사량 추정 알고리즘
2.3 태양광 발전량 예측 알고리즘
2.4 교차 검증
3. 실험 결과
3.1 모델 성능 평가
3.2 예측 알고리즘 적용 오차율 결과
4. 결론 및 고찰

Nomenclature

ANN : Artificial Neural Network

RNN : Recurrent Neural Network

NMAE : Normalized Mean Absolute Error

Subscript

$G_{b}$ : Direct solar radiation

$G_{d}$ : Solar diffusion

$G_{t}$ : All solar radiation

$C_{N}$ : Clearmess number

$θ$ : Weight or ANN parameter

$C o s t (θ)$ : Cost function

$α$ : Learning rate

$y_{i}$ : Actual value

${\hat{y}}_{i}$ : Forecast value

$n$ : Number of data points

$y_{\max}$ : Maximum of the actual value

$y_{\min}$ : Minimum of the actual value

1. 서 론

태양광 발전은 고갈되지 않는 친환경적인 에너지원이며, 시스템의 설치 및 가동이 빠르고, 유지보수가 편리하다는 등의 장점을 내세워 우리나라의 신재생에너지 중 가장 많은 누적 설치량 비중을 차지하고 있다^1,²⁾. 태양광 발전량은 조도, 온도, 습도, 구름 특성 등의 대기 변수에 의해 직간접적으로 영향을 받는다. 이러한 변수는 태양광 발전을 간헐적이고 가변성이 있는 특성을 갖게 한다. 따라서 점차 확대되는 태양광 발전이 전력망에 경제적이고 안정적으로 운영되기 위해서는 신뢰할 수 있는 예측 모델이 필요하다³⁾.

우리나라 역시 신재생에너지원 중 72.2%를 차지하는 태양광을 기존 송배전망에 연결할 때 이와 같은 단점으로 인한 문제를 방지하기 위하여 지난 2021년 발전량 예측제도를 도입하고 단점을 보완하고자 하였다⁴⁾.

낮시간에 발전이 이루어지는 태양광 발전은 발전이 이루어지는 시간대에 부하 감소로 인하여 덕커브(Duck curve) 현상이 발생한다. 이는 발전 출력의 급격한 증감발을 요구하며, 유연한 자원 확보를 필요로 한다⁵⁾. 신재생에너지 발전 규모가 지속적으로 확대됨에 따라서 기존 송배전망의 안정화 및 전력 공급과 수요의 효율적 관리가 점점 더 중요해지고 있다. 이러한 배경 하에, 2023년 6월에는 분산에너지의 활성화를 목표로 한 「분산에너지 활성화 특별법」이 제정되었다. 이 법에 따라 향후 우리나라를 비롯한 세계적인 에너지관리 체계는 중앙집중식 에너지 체계에서 지방분권 에너지 체계로 변화할 것이며, 이러한 배경에서 발전량 예측기술의 발전이 더욱 요구된다^6,⁷⁾.

그러나 그간의 태양광 발전량 예측은 설비용량에 지역적 평균 일사량 정보를 적용하는 방법부터 시작되어, 과거의 기상정보 및 기상예보를 활용하여 일사량을 예상하거나, 구름의 벡터값을 추정하여 계산된 태양에너지 복사의 예측 등을 활용하여 발전량을 예측하는 방법으로 발전되어 왔다. 이러한 방법은 지속성 및 통계적 방법을 기본으로 하는 수학적 모델로 발전량을 예측하는 까닭에 비선형 데이터 처리에 한계가 있었다^8,^9,^10,¹¹⁾. 이를 기반으로 최근에는 AI (Artificial Intelligence) 기술을 기반으로 과거의 기상 데이터, 지리 정보, 태양에너지의 복사량 등을 분석하여 최적의 발전량 예측을 하고자 하는 연구가 다수 진행되고 있다^12,^13,¹⁴⁾.

광기전력효과에 의해 발전이 이루어지는 태양광 발전의 예측에서 가장 중요한 변수는 일사량으로 표면 또는 태양광 모듈에 도달하는 일사량의 예측이 매우 중요하며 이에 대한 연구 역시 활발히 이루어지고 있다¹⁵⁾. 이에 본 연구에서는 먼저 실험 대상이 되는 발전소의 위치에 따른 일사량을 예측하고, 이를 반영하여 ANN (Artificial Neural Network)과 RNN (Recurrenct Neural Network)을 기반으로 한 신경망 알고리즘을 개발하여 정확도 높은 발전량을 예측하고자 하였다. 결과는 전력거래소(KPX)에서 요구하는 발전예측 인센티브 제도 방식에 따라 오차율을 검증하였다. 그 결과 1차(정산일 1일전 10시)에서 평균 7.40%, 2차(정산일 1일전 17시)에서 평균 7.03%의 오차율을 나타내었다.

2. 연구 방법

2.1 대기 상태에 따른 예측 모델 분리

태양광 발전량은 일반적으로 기온과 일사량의 변화에 따라 영향을 받으며, 기상청에서는 일사량에 대한 예보가 이루어지지 않기 때문에, Clear-Sky 모델에 의해 추정된 값을 사용한다. 이는 구름이 없는 맑은 하늘일 경우에 계산한 이론적인 일사량을 뜻한다. 따라서, 예측하고자 하는 일자에 태양광 발전소의 구름이 많거나 불규칙하다면 예측 모델에 의한 예측 오차는 커질 수 있다.

기상청에서 제공하는 대기 상태인 전운량을 기준으로 4가지의 대기 상태 예측 모델을 분리하여 각각의 하늘 상태 별로 학습 및 예측을 수행하였다. 기상청에서 제공하는 대기 상태를 Table 1과 같이 분류하였다.

Table 1.

Four models according to atmosphere conditions

State	Condition of weather
Class 1	Sunny
Class 2	Little Cloudy
Class 3	Cloudy
Class 4	Gray

2.2 일사량 추정 알고리즘

발전량 데이터의 경우 일사량과 밀접한 관련이 있으나, 기상청에서 다른 기상변수들과 다르게 정보를 제공하지 않고 있다. 따라서 태양광 발전소의 위치정보(경도, 위도)를 통해 기본 일사량에 대한 추정이 필요하다.

일사량 추정은 이론적 계산으로 널리 알려진 방법인 ASHRAE (American Society of Heating Refrigerating and Air-Conditioning Engineers) Clear-Sky 모델을 사용하여 지표면에 도달하는 일사량을 추정하였다. ASHRAE Clear-Sky 모델은 식 (1)을 이용하여 목표 지역의 직사량( $G_{b}$ ), 확산량( $G_{d}$ ), 지표면에 도달하는 일사량의 전량( $G_{t}$ )을 예측한다¹⁶⁾. 대기상태에 따른 일사량 변화를 적용하기 위해 청명도 상수( $C_{N}$ )를 적용하였고, 청명한 날 1.0을 기준으로 대기의 청명도가 떨어질수록 감소한다.

(1)

G_{N D} = \frac{A}{\exp (B / \sin α_{s})} C_{N}

(2)

G_{b} = G_{N D} \cos θ

(3)

G_{d} = C \times G_{N D}

(4)

G_{t} = G_{b} + G_{d}

2.3 태양광 발전량 예측 알고리즘

2.3.1 알고리즘 구조

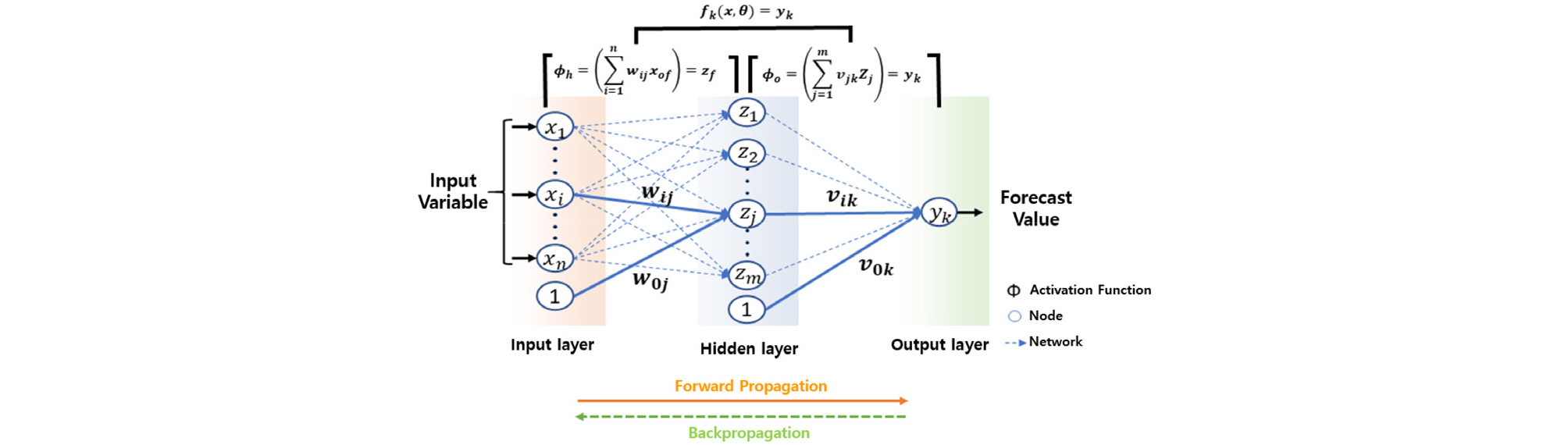
ANN-RNN 방식은 하이퍼파라미터 최적화가 알고리즘 내에 포함되어 있어 태양광 발전량 예측에 적합하다. 이 알고리즘의 구조는 입력층, 은닉층, 출력층 구조로 설계되어 있으며, 각 층간 최적 가중치를 탐색하는 알고리즘이다. ANN의 경우 하나 이상의 Perceptron이 여러 개의 층을 이룸으로써, 고차원의 데이터를 표현하는 방향으로 학습하여 예측을 수행한다¹⁷⁾. 본 연구에서 수행된 예측 수행 알고리즘을 Fig. 1과 같이 나타내었다.

https://cdn.apub.kr/journalsite/sites/cpr/2024-012-03/N0170120301/images/cpr_12_03_01_F1.jpg

Fig. 1

Photovoltaic generation forecast algorithm

발전량 예측 알고리즘에는 기상데이터(일사량, 기온, 습도, 구름량, 풍속), 시간 정보(시간, 일자, 계절), 태양광 모듈 특성(설치 각도), 태양광 발전량(과거 발전량 데이터)을 사용하여 입력층 데이터를 입력하였다.

입력층(ANN)을 비선형 전환을 통해 특성을 변환하고, 은닉층(ANN)에서 입력 데이터를 활용하여 패턴 및 데이터 특징을 추출한다. 그리고 ANN의 출력을 RNN으로 입력하고 시퀀스 데이터로 처리하여 시간 패턴을 학습한다. 이때 학습기법은 LSTM, GRU를 사용하였다. RNN의 출력은 ANN 출력층으로 전달되어 최종 예측 값을 생성한다.

이러한 ANN-RNN 방식은 인공 신경망과 순환 신경망의 장점을 결합하여 시계열 데이터에서 공간적 및 시간적 패턴을 동시에 학습이 가능하여 태양광 발전 예측과 같은 복잡한 문제를 해결하는데 유용하다.

2.3.2 알고리즘 순서도

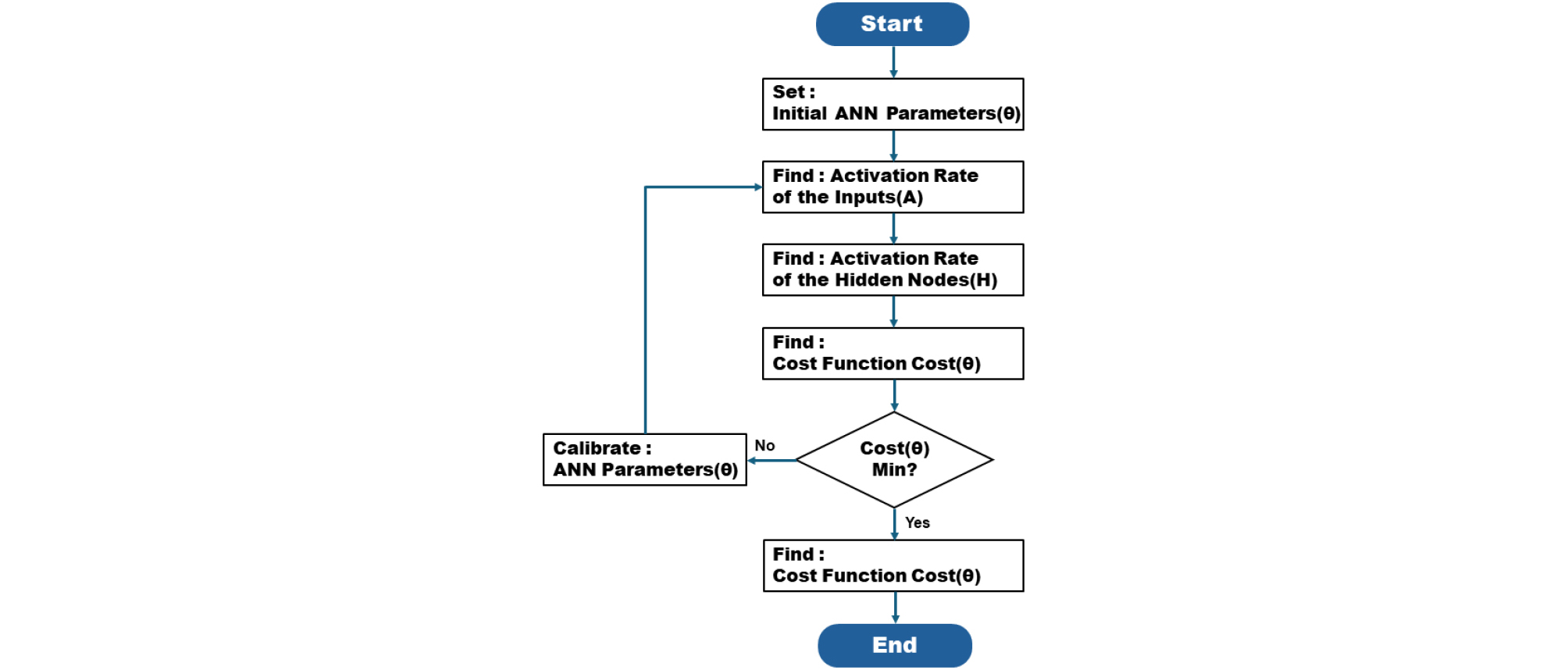
하이퍼파라미터는 은닉층의 노드수, 정규화 파라미터( $λ$ ) 및 랜덤 초기화 파라미터( $ε$ )가 있으며, 좋은 예측 성능을 도출하도록 적정한 값을 탐색한다. 하이퍼파라미터의 최적 조합 탐색을 위해 각 하이퍼파라미터별 비용함수(Cost Function)를 계산하여, 최소값이 발생하는 하이퍼파라미터 예측 모델 생성 학습 알고리즘 순서도는 Fig. 2와 같다.

https://cdn.apub.kr/journalsite/sites/cpr/2024-012-03/N0170120301/images/cpr_12_03_01_F2.jpg

Fig. 2

Photovoltaic generation forecast algorithm flow chart

비용함수는 모델의 성능을 평가하는 기준으로 값을 최소화하여 모델의 예측 정확도를 향상 시킨다. 비용함수의 값을 줄여 실제값과 가까워지도록 보다 정확한 예측값을 도출할 수 있고, 파라미터 및 가중치 조정을 통해 모델 성능을 개선할 수 있다. 또한 데이터에 대한 학습이 과하게 수행됨에 따라 오차가 증가할 수 있는 문제를 가지고 있는 과적합(overfitting)을 방지할 수 있다.

하이퍼파라미터 최적화 기법으로는 경사하강법(Gradient descent)이 적용되었으며, 식 (5)을 이용하여 최적화를 수행하였다.

(5)

θ_{t + 1} = θ_{t} - α \nabla C o s t (θ_{t})

2.4 교차 검증

학습 데이터에 대해서만 과도하게 학습되는 과적합을 방지하기 위해 파라미터들이 최적의 값으로 설정되었는지 평가하기 위하여 교차 검증을 실시하였다.

모델 평가는 학습 데이터로 사용되는 데이터를 학습 세트와 테스트 세트로 나누어 평가하였다. 학습 세트에서의 오차(Cost)가 낮지만 일반화 오차(새로운 데이터에 대한 오류 비율)가 높다면 모델이 훈련 데이터에 과적합 되었다는 것을 의미하므로, 최대한 많은 데이터를 가지고 검증을 수행하기 위해 교차 검증 방법을 이용하였다.

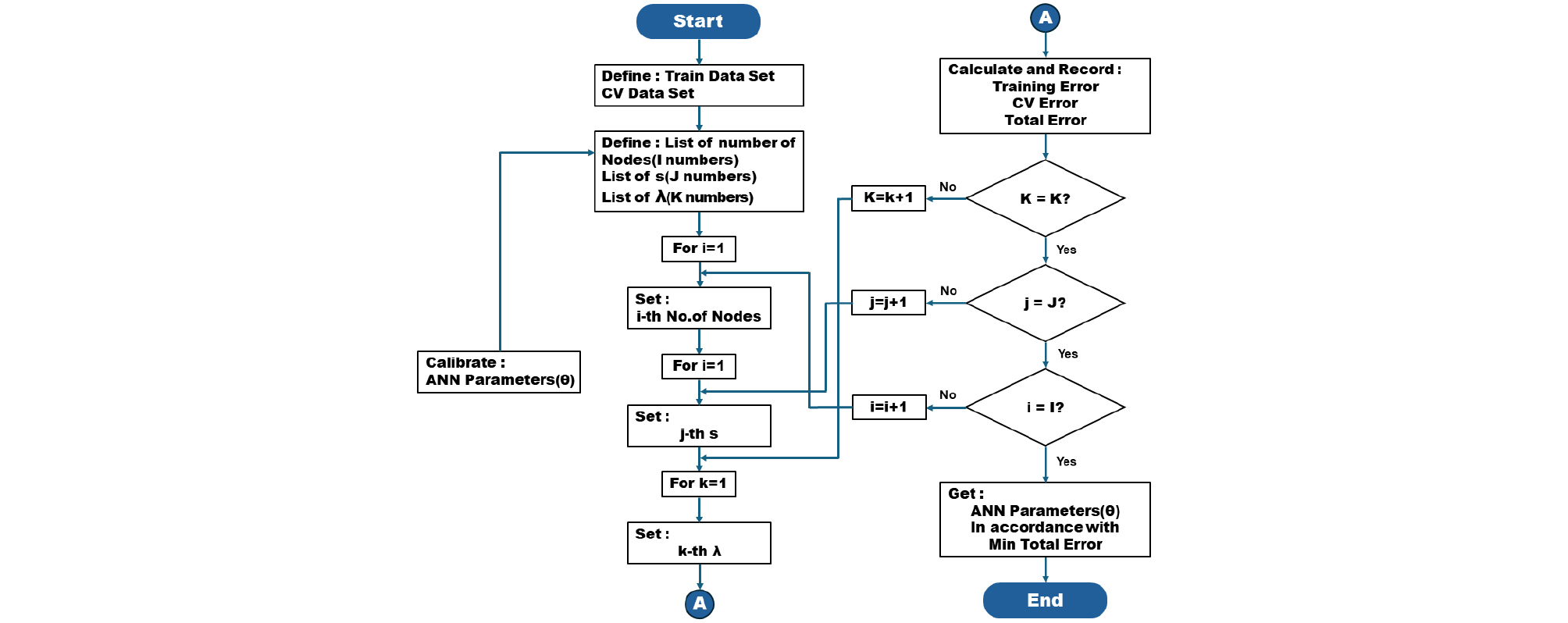
교차 검증 방법은 데이터 집합을 학습 데이터 집합, 교차 검증 데이터 집합, 테스트 데이터 집합의 세 가지 집합으로 나누고, 각각을 나눈 집합을 교차하여 다시 검증하고 일반화 오차 평균값을 이용하여 최적 하이퍼파라미터를 선택하였으며, 교차 검증 순서도는 Fig. 3과 같다.

https://cdn.apub.kr/journalsite/sites/cpr/2024-012-03/N0170120301/images/cpr_12_03_01_F3.jpg

Fig. 3

Cross validation flow chart

3. 실험 결과

3.1 모델 성능 평가

본 예측 알고리즘에서 하이퍼파라미터 셋은 아래와 같이 설정하였다.

- 은닉층의 수 : best result(7)

- 초기화 파라미터( $ε$ )

$ε = \{0.01 \times \{2^{0}, 2^{1}, 2^{2}, 2^{3}, 2^{4}, 2^{5}, 2^{6}, 2^{7}\}\} = \{0.01, 0.01, 0.04, 0.08, 0.16, 0.64, 1.28\}$

- 정규화 파라미터( $λ$ )

$λ = \{0.01 \times \{e^{0}, e^{1}, e^{2}, e^{3}, e^{4}, e^{5}, e^{6}, e^{7}\}\} = \{0.01, 0.03, 0.07, 0.2, 0.5, 1.5, 4, 11\}$

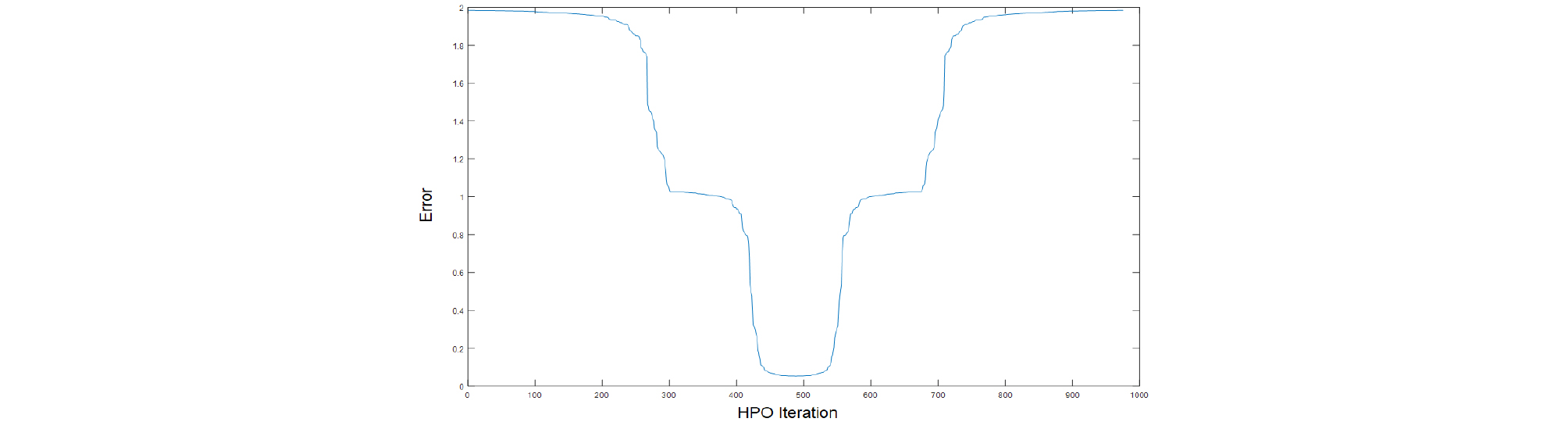
하이퍼파라미터 최적화를 위하여 모델을 선정하고 데이터의 수집, 분류 및 처리 과정으로 전처리를 하여 Grid Search, Randum Search, Hyperband 등의 기법으로 최적화를 진행하였다. 훈련 및 검증을 통해 하이퍼파라미터를 선택하였고, 그 결과를 Fig. 4와 같이 나타내었다.

https://cdn.apub.kr/journalsite/sites/cpr/2024-012-03/N0170120301/images/cpr_12_03_01_F4.jpg

Fig. 4

Hyperparameter optimization results

3.2 예측 알고리즘 적용 오차율 결과

연구된 알고리즘을 2021년 12월~2022년 12월 1년의 보유 데이터를 활용하여 예측값과 실제값 사이의 절대 오차의 평균을 의미하는 NMAE의 평균 값으로 월별 결과를 도출하였다. 전력거래소의 발전예측 인센티브 제도를 적용하여 1차, 2차의 예측 오차율 결과를 도출한 결과는 각각 Table 2와 3과 같다.

Table 2.

Error rate results for the first submission (10:00 AM the day before)

Division		A	B	C
Capacity (kWp)		947	1,187	476
NMAE (%)	21Y 12M	7.5	7.3	6.8
	22Y 1M	7.4	7.9	7.6
	22Y 2M	8.2	8.8	6.6
	22Y 3M	6.9	8.4	7.7
	22Y 4M	7.8	10.5	5.6
	22Y 5M	6.3	8.7	5.4
	22Y 6M	7.2	7.4	7.8
	22Y 7M	8.4	6.1	8.4
	22Y 8M	9.4	8.8	8.1
	22Y 9M	7.5	6.9	8.2
	22Y 10M	7.9	6.5	6.6
	22Y 11M	6.6	5.3	5.6
	22Y 12M	7.8	7.7	5.2
Average of ‘NMAE’		7.6	7.7	6.9

Table 3.

Error rate results for the second submission (05:00 PM the day before)

Division		A	B	C
Capacity (kWp)		947	1,187	476
NMAE (%)	21Y 12M	7.5	6.9	6.3
	22Y 1M	7.4	7.7	7.0
	22Y 2M	7.5	8.7	5.9
	22Y 3M	6.5	8.2	7.5
	22Y 4M	7.6	10.5	5.5
	22Y 5M	5.9	7.7	4.8
	22Y 6M	6.8	7.2	7.6
	22Y 7M	8.4	6.1	8.4
	22Y 8M	8.6	8.5	7.1
	22Y 9M	7.1	6.6	8.1
	22Y 10M	7.7	6.3	6.5
	22Y 11M	6.1	5.1	5.0
	22Y 12M	6.9	7.2	4.8
Average of ‘NMAE’		7.2	7.4	6.5

표에는 발전소별 설치용량(Capacity)과 데이터가 너무 방대하기 때문에 일별 오차율 평균을 한달 주기(00Y-00M)로 오차율값을 정리하였다. 위치 및 용량별 차이가 있는 발전소를 A, B, C로 구분하였다. 본 연구에서 태양광 발전 예측은 대기상태에 따른 일사량이 예측된 기반으로 결과를 도출하고 있음에 따라 월별 오차율의 편차가 발생한 원인으로 일사량 예측 오차 요인이 작용한 것으로 사료된다.

(6)

N M A E = \frac{\sum_{i = 1}^{n} |y_{i} - \hat{y}|}{n \cdot (y_{\max} - y_{\min})}

태양광 발전의 여러가지 변수중에 가장 큰 영향을 미치는 변수중의 하나인 일사량을 추정하여 발전량 예측 알고리즘에 적용한 결과는 발전량 예측 제도에서 요구되는 8% 이내의 오차율을 모두 나타내었다. 특히 475 kWp급 발전소에서는 6% 대의 1차(정산일 1일전 10시) 오차율을 나타내어 유의미한 결과를 도출할 수 있었다. 이에 습도, 온도, 미세먼지 등의 또 다른 태양광 발전의 변수를 적용하는 연구나 용량을 분할하여 발전량을 예측하고 합산 과정에서의 손실 및 오차를 보완하는 등의 연구를 연계하면 더욱 낮은 오차율을 달성할 수 있을 것으로 보인다.

2차(정산일 1일전 17시) 오차율 예측 결과는 각각 0.4, 0.3, 0.4%의 오차율이 향상되는 경향의 결과가 도출되었다. 오차율이 향상된 요인은 11시부터 15시까지 예측 편차가 가장 높게 발생하는데 2차 발전량 예측의 경우 해당 시간의 실 발전 데이터를 한 번 더 사용함에 따라 오차율을 향상 시켰다고 볼 수 있다. 이러한 배경에서 또다른 고급 기상 모델을 적용하거나 여러 기상 데이터를 통합하여 결과를 향상 시킬 수 있을 것이다.

또한 1, 2차 결과 모두에서 발전소의 출력이 상대적으로 대용량일수록 오차율이 비례하여 높은 경향을 나타내었다. 이는 태양광 발전의 또 다른 단점인 넓은 부지를 필요로 한다는 점과 연관성이 있는 것으로 사료된다. 예측된 일사량이 적용되는 면적을 초과할수록 오차율이 점차 커진다는 뜻이다.

이러한 문제를 해결하기 위해 복사각도 및 면적을 계산하여 동일한 일사량을 적용할 수 있는 태양광발전소 면적을 정의하고, 이를 단위별 발전량 예측 및 합산하는 방식의 추가 연구가 진행된다면 발전량 예측의 정확도를 향상 시키는데에 보다 의미 있는 기여를 할 수 있을 것으로 사료된다.

4. 결론 및 고찰

대표적인 신재생에너지원인 태양광의 오차율이 적은 발전량 예측을 위하여 다양한 변수 접근과 인공지능기술을 접목하여 많은 연구가 진행되고 있다. 보다 정확한 발전량 예측을 통해 안정적인 전력운영을 할 수 있고, 발전사업자 측면에서는 발전량 예측 시장을 통해 추가적인 수입을 창출 할 수 있다. 이에 본 연구에서는 태양광 발전량 예측에 영향을 미치는 수많은 변수 중 가장 큰 공신력을 갖는 기상청 정보를 기반으로 하는 일사량을 예측하여 6.5~7.7% 수준의 정확도 높은 발전량 예측 결과를 도출하였다.

ANN 모델의 방식은 이미지 인식, 텍스트 분류, 일반적인 회귀 분석 등과 같은 정적인 데이터의 분류나 회귀 문제를 해결하는데 사용되지만, 시계열 데이터나 시간적 의존성을 처리하는데에는 한계가 있다. RNN 모델은 자연어 처리, 음성 인식, 주가 예측 등과 같은 시퀀스 데이터 처리와 이전 시간 스텝의 정보를 기억하고 현재 시간 스텝의 입력과 결합하여 출력한다. 하지만 장기적인 의존성을 학습하는데 한계가 있고, 기울기 소멸 문제가 야기된다. 따라서 본 연구에서는 ANN과 RNN 모델을 결합하는 하이브리드 모델을 적용하여 발전량 예측을 하고자 하였다. 공간적(ANN)과 시간적(RNN) 패턴을 동시에 학습하여 복잡한 시계열 데이터로부터 높은 발전량 예측 결과를 얻을 수 있었다.

본 연구 결과로 8% 이내의 오차를 요구하는 발전량 예측시장에 즉각적인 대응이 가능하며, 1년간의 발전데이터를 기반으로 이루어진 본 연구가 다년간의 발전데이터를 기반으로 한 연구로 확대된다면 그 오차율이 더 감소할 수 있을 것으로 보인다. 이 외 변수인 온도, 습도, 미세먼지, 풍량 및 풍속 등을 접목한 연계 연구를 통해 발전량 예측의 정확도를 더욱 향상할 수 있을 것으로 예상된다. 또한 향후 최소한의 오차율을 도출하는 연구와 더불어 부하, 즉 전력의 수요분석을 통해 공급과 수요를 일치시키는 방법이나 에너지저장장치를 이용하여 충방전을 활용한 오차율 최소화와 관련된 연계 연구가 필요할 것으로 사료된다.

Acknowledgements

본 결과물은 2024년도 교육부의 재원으로 한국연구재단의 지원을 받아 수행된 지자체-대학협력 기반 지역혁신 사업의 결과입니다(2021RIS-002).

본 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다(RS-2024- 00358809).

References

Korea Energy Agency (KEA), 2022 New and Renewable energy supply statistics final results (2023. 12).

P. R. Brown, F. M. O'Sulivan, Shaping photovoltaic array output to align with changing wholesale electricity price profiles. Appl. Energy. 256, 113734 (2019).

10.1016/j.apenergy.2019.113734

M. S. Hossain, H. Mahmood, Short-term photovoltaic power forecasting using an LSTM neural network and synthetic weather forecast. IEEE. ISSN 2169-3536, DOI 10.1109/ACCESS.2020.3024901 (2020).

10.1109/PECI48348.2020.9064654

KPX, Electricity market operation rules.

G. M. Pitra, K. S. Sastry Musti, Dcuk curve with renewable energies and storage technologies, 13th International Conference on Computational Intelligence and Communication Networks, Lima, Peru, doi:10.1109/CICN51697.2021.13 (2021).

10.1109/CICN51697.2021.9574671

K. S. Kwon, Review of the special act on the promotion of distributed energy (Proposal), KLGLA, Vol. 77, No. 23-1 (2023).

W. S. Kim, H. H. Jo, Impact of photovoltaic generation expansion on Korea's electricity power system and the solution: Focusing on power system stability and supply and demand stability. KJECON. 27, 23-65 (2020).

10.46228/KJE.27.1.2

H. Huang, J. Xu, Z. Peng, S. Yoo, D, Yu, D. Huang, H. Qin, Cloud motion estimation for short term solar irradiation prediction, SmartGrid Communications IEEE International Conference, pp. 696-701 (2013).

10.1109/SmartGridComm.2013.6688040

J. J. Song, Y. S. Jeong, S. H. Lee, Analysis of prediction model for solar power generation. J. of Digital Convergence. 12, 243-248 (2014).

10.14400/JDC.2014.12.3.243

K. D. Kim, The development of the short term predict model for solar power generation. KSES. Vol. 33, No. 6 (2013).

10.7836/kses.2013.33.6.062

H. J. Na, K. S. Kim, Study on generation volume of floating solar power using historical insolation data. JKSCE. 43, 249-258 (2023).

A. Mohammad, F. Mahjabeen, Revolutionizing solar energy: The impact of artificial intelligence on photovoltaic systems. J. Multidiscip. Res. 2, 117-127 (2023).

10.47709/ijmdsa.v2i1.2599

C. L. Sergio, M. C. Ricardo, C. David, A. George, Deep and machine learning models to forecast photovoltaic power generation. Energies. 16, 4097 (2023).

10.3390/en16104097

J. I. Lee, W. K. Park, I. W. Lee, S. H. Kim, Comparison of solar power prediction model based on statistical and artificial intelligence model and analysis of revenue for forecasting policy. KIEEME. 26, 335-363 (2022).

F. Antonanzas-Torres, R. Urraca, J. Polo, O. Perpinan-Lamigueiro, R. Escobar , Clear sky solar irradiance models: A review of seventy models. Renewable Sustainable Energy Rev. 107, 374-387 (2019).

10.1016/j.rser.2019.02.032

J. H. Kim, M. H. Kim, O. H. Kwon, Y. J. Seok, J. W. Jeong, Generation of monthly averaged horizontal radiation based on a regional clearness estimatimg model. KSES. 30 (2010).

Y. T. Lee, D. H. Kim, W. S. Sin, C. K. Kim, H. G. Kim, S. W. Han, A comparison of machine learning models in photovoltaic power generation forecasting. KIIE. 47, 444-458 (2021).

10.7232/JKIIE.2021.47.5.444

Current Photovoltaic Research ISSN:2288-3274(Print) 2508-125X(Online)

Preview

A Study on ANN/RNN-based Photovoltaic Generation Forecasting

ABSTRACT

MAIN

Table 1.

Four models according to atmosphere conditions

(1)

(2)

(3)

(4)

Fig. 1

Photovoltaic generation forecast algorithm

Fig. 2

Photovoltaic generation forecast algorithm flow chart

(5)

Fig. 3

Cross validation flow chart

Fig. 4

Hyperparameter optimization results

Table 2.

Error rate results for the first submission (10:00 AM the day before)

Table 3.

Error rate results for the second submission (05:00 PM the day before)

(6)

Acknowledgements

References